Importance sampling

This post is about importance sampling. For importance sampling, although it seems to be a sampling method as its name suggests, it is actually a method for estimating the expectation $\mathbb{E}$ of some certain function $f(z)$ w.r.t a probability distribution $p(z)$.

\[\mathbb{E}(f) = \int p(z) f(z) dz\]

One simple strategy is to take discretised $z$ values in $z$-space uniformly and the expectation above is approximated by

\[\mathbb{E}(f) \approx \sum_{l=1}^{L} p(z^{(l)}) f(z^{(l)})\]

However, it is inefficient because small value of $p(z^{(l)}) f(z^{(l)}) $ attributes few for the expectation $\mathbb{E}(f)$. Only a small region of $z$ makes contribution to the sum. As the dimensionality of $z$ grows, the situation will get worse.

As we do in rejection-sampling, in importance sampling we also have propose distribution $q(z)$, which is easy to take samples from it. The expectation $\mathbb{E}(f)$ is reformulated.

\[\begin{align} \mathbb{E}(f) &= \int f(z) p(z) dz \nonumber \\ &= \int f(z) \frac{p(z)}{q(z)} q(z) dz \\ & \approx \frac{1}{L}\sum_{l = 1}^{L} \frac{p(z^{(l)})}{q(z^{(l)})} f(z^{(l)}) \end{align}\]

In this approximation, the samples $z$ for calculating $\mathbb{E}(f)$ are from propose distribution $q(z)$. Under the assumption that we can easily evaulate $\tilde{p}(z) = Z_p p(z)$ and $\tilde{q}(z) = Z_q q(z)$, we reformulate the approximation of $\mathbb{E}(f)$ again.

\[\begin{align} \frac{1}{L}\sum_{l = 1}^{L} \frac{p(z^{(l)})}{q(z^{(l)})} f(z^{(l)}) &= \sum_{l = 1}^{L} \frac{Z_p * \tilde{p}(z^{(l)})}{Z_q * \tilde{q}(z^{(l)})} f(z^{(l)}) \nonumber \\ &= \frac{Z_q}{Z_p} \sum_{l = 1}^{L} \tilde{r_l}f(z^{(l)}) \\ &= \frac{\sum_{l = 1}^{L} \tilde{r_l}f(z^{(l)})}{Z_p/Z_q} \end{align}\]

where $\tilde{r_l} = \frac{\tilde{p}(z^{(l)})}{\tilde{q}(z^{(l)})}$.

We call $r_l$ importance weight. For $Z_p/Z_q$, we have

\[\begin{align} \frac{Z_p}{Z_q} &= \int \frac{\tilde{p(z)}}{Z_q q(z)} q(z) dz \\ &= \int \frac{\tilde{p(z)}}{\tilde{q(z)}} q(z) dz \\ & \approx \frac{1}{L}\sum_{l=1}^{L}\tilde{r_l} \end{align}\]

Based on the approximation of $Z_p/Z_q$ and $\mathbb{E}(f)$, we have

\[\begin{align} \mathbb{E}(f) & \approx \frac{\sum_{l = 1}^{L} \tilde{r_l}f(z^{(l)})}{\sum_{l=1}^{L}\tilde{r_l}} \\ & \approx \sum_{l=1}^{L} w_l f(z^{(l)}) \end{align}\]

where $w_l = \frac{\tilde{r}_l}{\sum_{m=1}^{L}\tilde{r}_m}$.

One remark is that when using importance sampling, the propose distribution $q(z)$ is important. If the region where $p(z)* f(z)$ has large value doesn’t match the region where samples from $q(z)$ are concentrated, the approximation may be quite wrong. For example, $f(z) = e^{|z|}$, $p(z) \sim \mathbb{N}(0, 3^2)$, $q(z) \sim \mathbb{N}(10, 1^2)$ and $Z_p = 4, Z_q = 2$. The figure below shows the general overview.

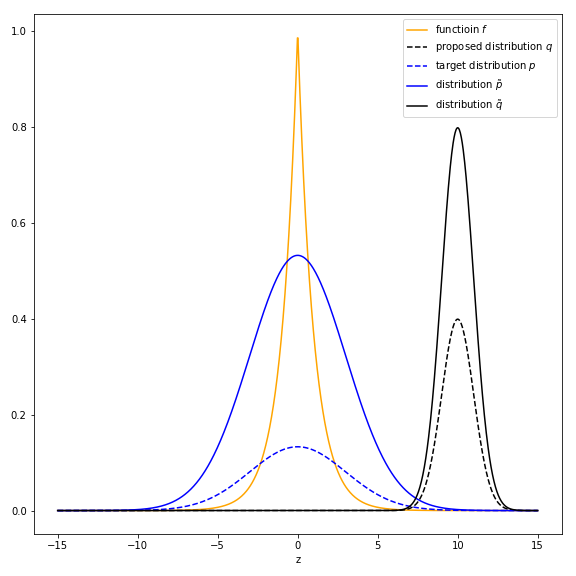
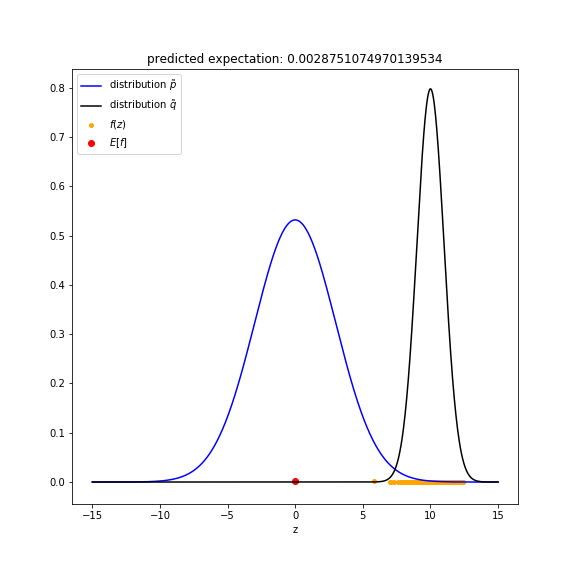
The approximation of using importance sampling is the y-axis value of the red point in the figure. It is also the title of the figure. The orange points are the sampled points $z$ from $q(z)$ and their corresponding $f(z)$.

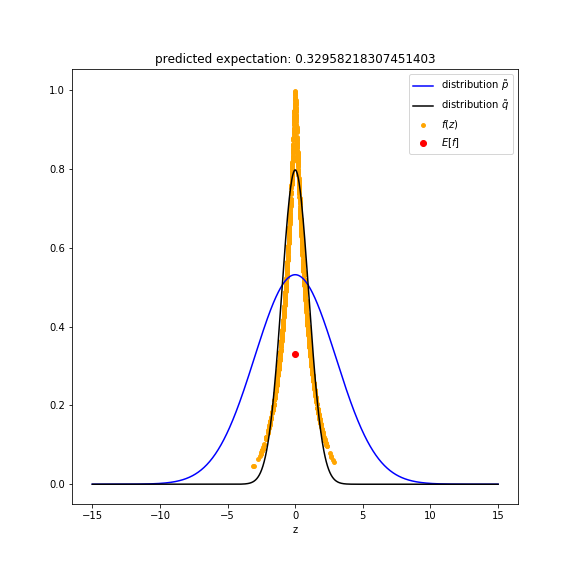
If we choose $q(z) \sim \mathbb{N}(0, 1^2)$, then the approximation is much better.

More programming details are in this notebook

Based on the $r_l$ importance weights, there exists a method for sampling from desired distribution $p(x)$. It is called sampling-importance-resampling. It has a very important real-world application, particle filter. Since it is not a small topic, I am going to write another post about sampling-importance-resampling with some interesting applications using particle filter.