Strongly connected component and Tarjan Algorithm
In a directed graph, a graph is said to be strongly connected if there is a path from every vertex to every other vertex. The strongly connected components (SCCs) of a directed graph are subgraphs where each subgraph is strongly connected, meaning every node can reach every other node in that subgraph. These SCCs form a partition of the graph into smaller, strongly connected subgraphs.
One of the most efficient algorithms for finding SCCs is Tarjan Algorithm. This algorithm is based on Depth-First Search (DFS) and can identify all the SCCs in a graph in linear time. However, to understand Tarjan algorithm, we first need to cover some foundational concepts.
DFS Tree
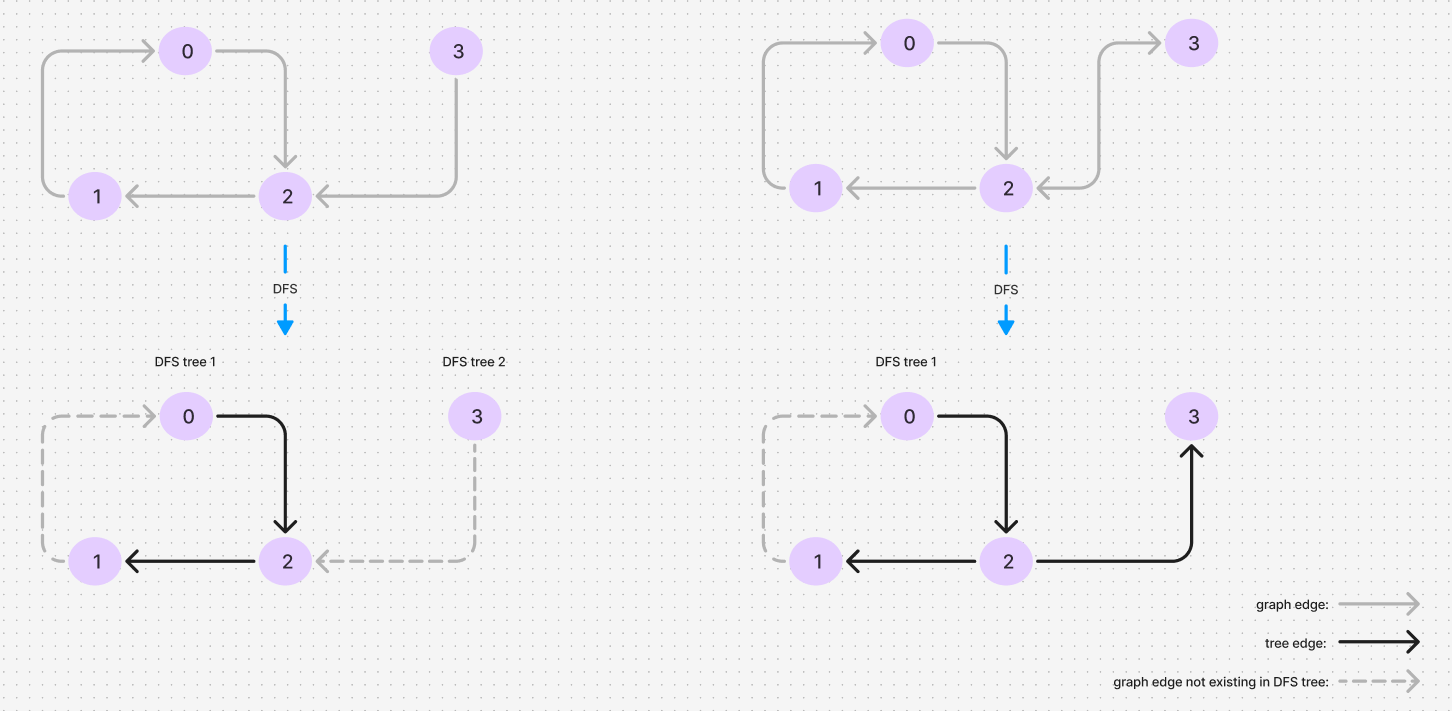
When we perform a DFS on a directed graph, the traversal can be organized into a collection of trees called DFS trees. These trees represent the nodes visited during the DFS. Importantly, nodes that belong to different DFS trees cannot be part of the same SCC, even if they are connected.
The chart below on the left shows the resulting 2 DFS trees after DFS, where vertex 2 and 3 are connected in the graph but they don’t form a SCC. While on the right, there is only 1 DFS tree after DFS, where vertex 2 and 3 form a SCC.
Back Edges and Cross Edges
Once we have the DFS tree, the edges of the graph can be classified into different types:
- Forward edges: Point from a node in the tree to one of its descendants.
- Back edges: Point from a node to one of its ancestors.
- Cross edges: Neither a forward nor a back edge; they connect nodes between different branches or subtrees.
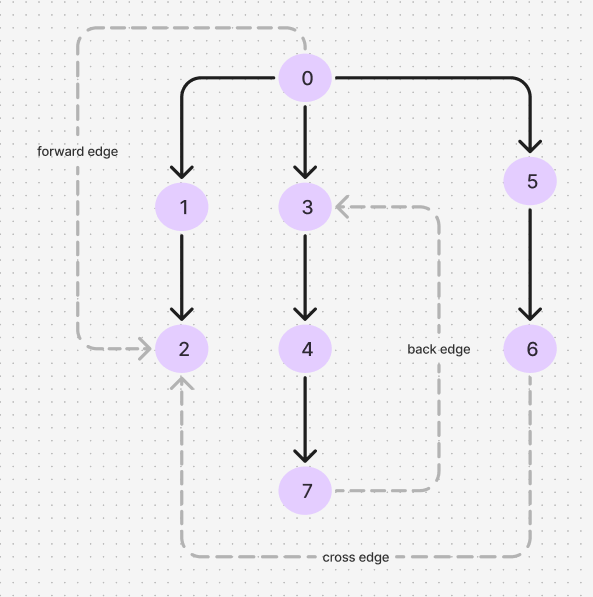
A back edge points to an ancestor in the DFS tree that hasn’t yet been fully explored. In contrast, a cross edge points to a node that has either already been fully explored or hasn’t been visited at all.
The key to finding SCCs is identifying back edges in the DFS tree, as they indicate a cycle in the graph—one of the core features of an SCC.
Tarjan Algorithm
In standard DFS, we use a set to track visited nodes to prevent infinite recursion. However, Tarjan algorithm needs more than that—it must distinguish between back edges and cross edges, and keep track of nodes involved in SCCs. To achieve this, we introduce a stack and two arrays.
Two Arrays Used:
- Traversal Order Array (ID): This array stores the order in which nodes are visited during DFS. The node that starts the DFS gets an ID of 0, its first neighbour gets an ID of 1, and so on. By setting all initial values to -1, this array can also track whether a node has been visited.
- Low-Link Array: This array tracks the smallest ID reachable from each node within the same SCC. Initially, a node’s low-link value is set to its traversal ID. However, as DFS explores deeper nodes, this value may be updated to reflect connections within SCCs.
Consider a strongly connected component (SCC) shown below.
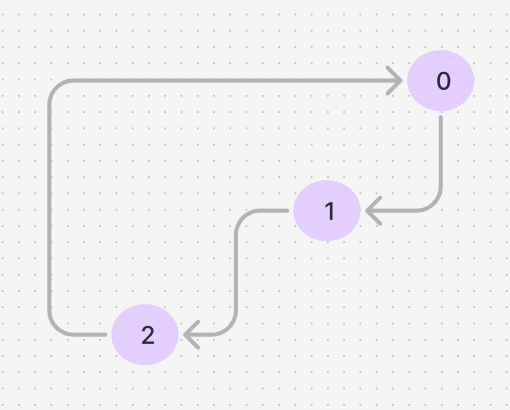
If we start DFS from node 0, the ID for nodes 0, 1, and 2 would be 0, 1, and 2, respectively. The low-link values should ideally be $[0, 0, 0]$ in the end, indicating that all these nodes are part of the same SCC. The node with the same ID and low-link value is considered the root of the SCC. The GIF below illustrates this process.
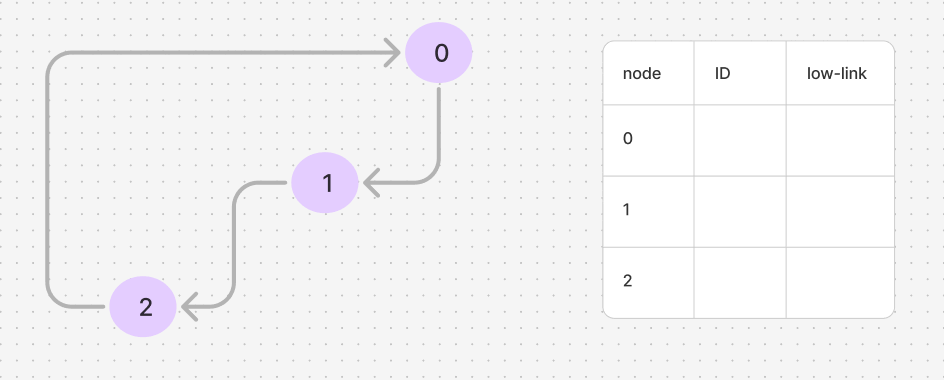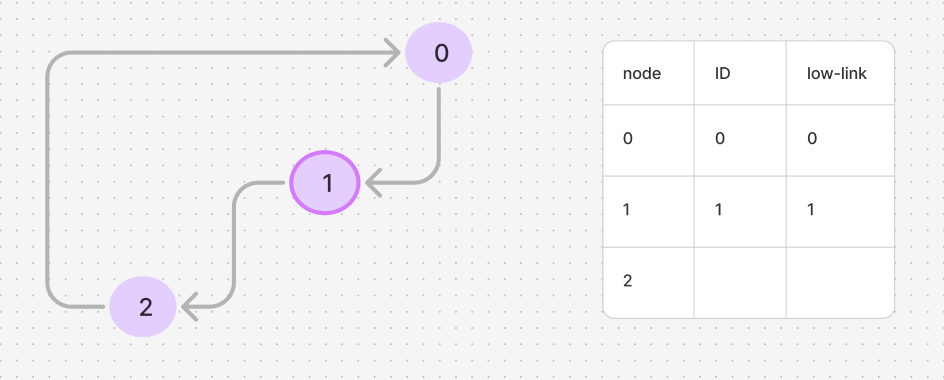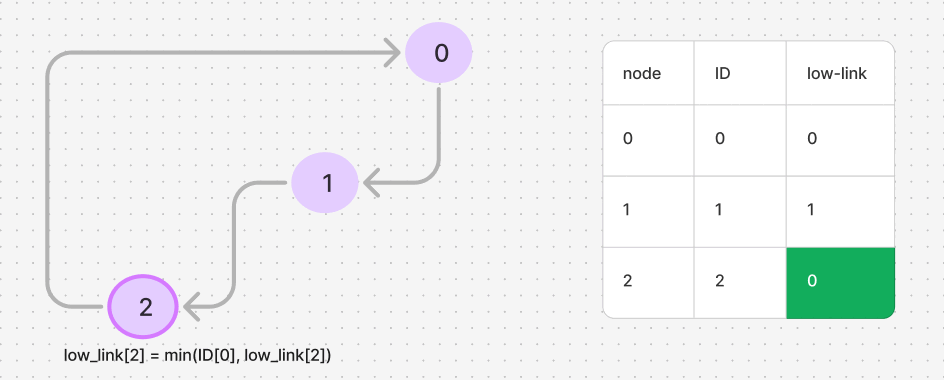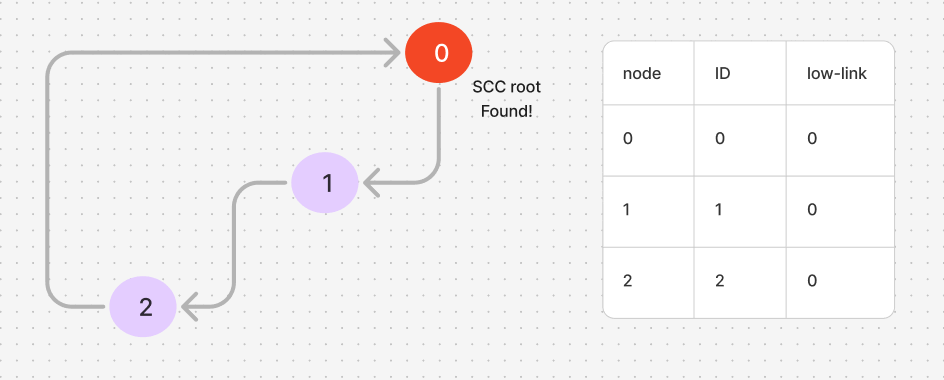
Below is an example of how this process is implemented in code.
for neighbor in node:
# If the neighbor is not visited
if neighbor not visited:
recursion_function(...)
low_link[node] = min(low_link[node], low_link[neighbor])
# Back edge case
elif is_back_edge(node, neighbor):
low_link[node] = min(low_link[node], ID[neighbor])
A Stack Used
The unknown function is_back_edge in the code above can be defined using the stack. The stack helps distinguish between back edges and cross edges.
When visiting a node, it is pushed onto the stack. Once we encounter a node where its low-link value equals its ID (the root of an SCC), we pop all nodes from the stack until we reach that node. The nodes that are popped form an SCC. This approach ensures the stack only contains nodes from non-fully explored DFS subtrees.
Because of the way the stack is maintained, a back edge always points to a node still in the stack, while a cross edge points to a node that is not in the stack. By checking if a neighbour is in the stack, we can determine whether the edge is a back edge or a cross edge.
if low_link_list[node] == index_list[node]:
tmp_res = []
while stack:
tmp_node = stack.pop()
tmp_res.append(tmp_node)
on_stack[tmp_node] = False
if tmp_node == node:
break
res.append(tmp_res)
Key Steps in Tarjan Algorithm:
- For each node in the graph, if it has not been visited, perform a DFS from that node.
- During the DFS:
- Assign an ID to the node and set its low-link value.
- Push the node onto the stack.
- For each neighbour of the node:
- If the neighbour has not been visited, recursively perform DFS on the neighbor, and update the low-link value of the current node based on the low-link value of the neighbour.
- If the neighbour is still in the stack (indicating a back edge), update the low-link value of the current node.
- When a node’s low-link value equals its ID, it indicates that this node is the “root” of an SCC. Pop all nodes from the stack until the current node is reached. These nodes form an SCC.
Full Implementation:
Here’s the full code implementation for Tarjan SCC algorithm:
# ID array
index_list = [-1 for _ in range(num_nodes)]
# Low-link array
low_link_list = [-1 for _ in range(num_nodes)]
# Stack tracking nodes
on_stack = [False for _ in range(num_nodes)]
stack = []
# Array to store SCCs
res = []
def tarjan_scc(node, graph, index, index_list, low_link_list, stack, on_stack):
# Set ID and low-link for the current node
index_list[node] = index
low_link_list[node] = index
stack.append(node)
on_stack[node] = True
index += 1
# Perform DFS on neighbors
for neighbor in graph.adj_list[node]:
if index_list[neighbor] == -1:
index = tarjan_scc(neighbor, graph, index, index_list, low_link_list, stack, on_stack)
low_link_list[node] = min(low_link_list[node], low_link_list[neighbor])
elif on_stack[neighbor]:
low_link_list[node] = min(low_link_list[node], index_list[neighbor])
# If the node is an SCC root, pop all nodes in the SCC
if low_link_list[node] == index_list[node]:
tmp_res = []
while stack:
tmp_node = stack.pop()
tmp_res.append(tmp_node)
on_stack[tmp_node] = False
if tmp_node == node:
break
res.append(tmp_res)
return index