Union-Find Problems in Leetcode
The Union-find data structure also called a disjoint-set data structure, is a data structure that stores a collection of disjoint sets.
This data structure helps us to solve graph-related problems, for example finding groups of connected components in a graph, which is LC 547. Number of Provinces. As long as the problem asks you to find one or more sets containing non-overlapping elements, a disjoint set might be helpful. e.g. LC 128. Longest Consecutive Sequence.
find and union method
The data structure has two methods. find and union. Method find returns the root of the given element. Method union finds the root of each node and make one root become the parent of another root.
find with path compression
Imagine we have one node in the disjoint set. Every time we union a new node to that node, the length/height increases. This means that if we call the find method, we need to go through all the added nodes, which is O(n) time complexity.
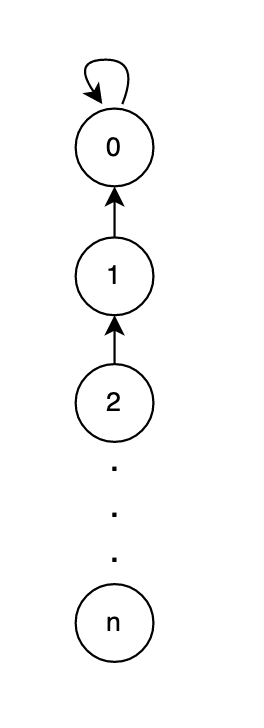
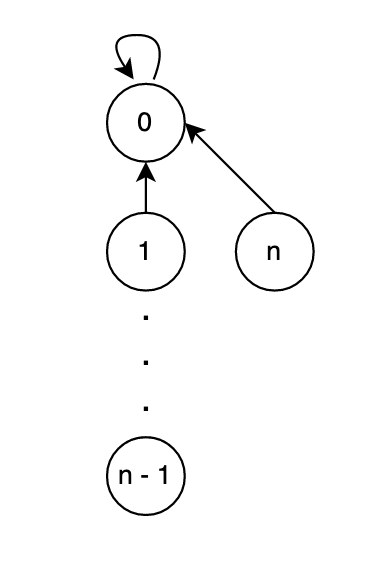
To avoid this cost, the find method is implemented with path compression. With path compression, every time we call the find method, the updated root is stored and then returned. So next time when we use find, it takes only a constant time.
union by rank
rank is an attribute that every node in the disjoint set has. It is initialized with 0.
A node’s rank is added by 1 only when this node is unioned with another node and both nodes have the same rank. When a union happens between two nodes whose parents have different ranks, the parent node with a higher rank becomes another parent node’s parent but its rank remains unchanged.
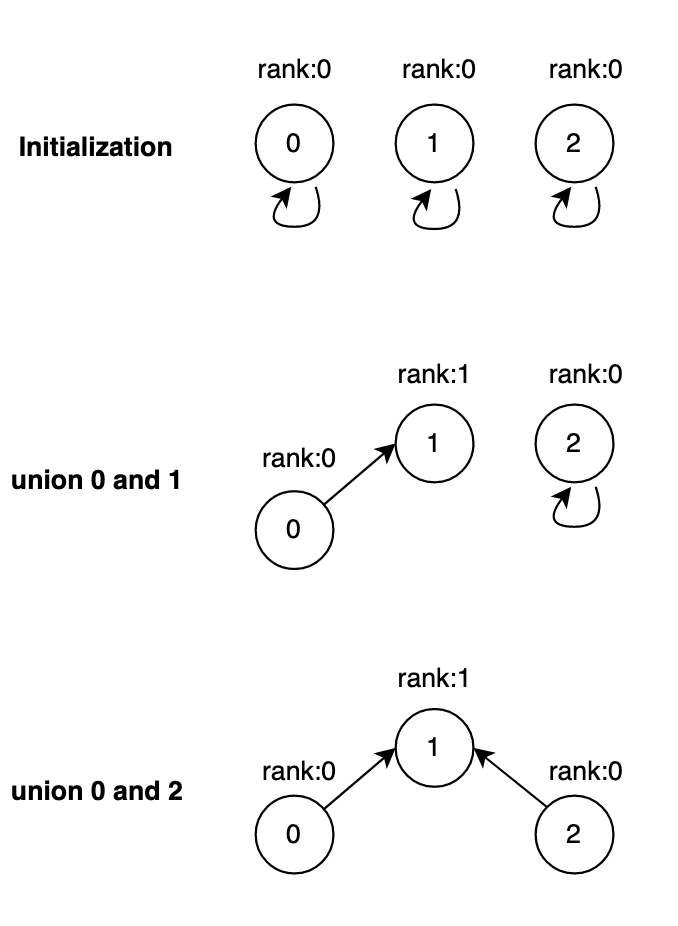
If we naively do union, for example always making the first node the parent node for the second node. The height of the tree grows linearly. Even though we have the method find with path compression, the first time calling the find method takes O(n) time complexity still.
Union-Find with path compression and union-by-rank Template
class DisjointSet:
def __init__(self, num_nodes):
self.parents = [i for i in range(num_nodes)]
self.rank = [0 for _ in range(num_nodes)]
def find(self, node):
if self.parents[node] == node:
return node
self.parents[node] = self.find(self.parents[node])
return self.parents[node]
def union(self, node1, node2):
parent1 = self.find(node1)
parent2 = self.find(node2)
if parent1 == parent2:
return
if self.rank[parent1] == self.rank[parent2]:
self.parents[parent2] = parent1
self.rank[parent1] += 1
elif self.rank[parent1] > self.rank[parent2]:
self.parents[parent2] = parent1
else:
self.parents[parent1] = parent2
Without optimizations in find and union, both methods have a time complexity of O(n).
With the only union by rank, both methods have a time complexity of O(logn)
With union by rank and path compression, both methods have a time complexity of O(1).
It is trivial to see that the time complexity of union depends on the find method. And find method’s time complexity depends on the tree height. Without union by rank, as nodes get unioned, the height of the tree grows linearly in the worst case. Union by rank stops the linear growth of the height. And every node’s rank doesn’t exceed log2(n). The ranks of the nodes in a path from a given node to its root are strictly increasing. So the time complexity is O(logn).
Here are some union-find problems and solutions from leetcode.
LC. 547 Number of Provinces
class DisjointSet:
def __init__(self, n):
self.parent = [i for i in range(n)]
self.rank = [0 for _ in range(n)]
def find(self, x):
if self.parent[x] == x:
return x
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
x_p = self.find(x)
y_p = self.find(y)
if self.rank[x_p] == self.rank[y_p]:
self.parent[x_p] = y_p
self.rank[y_p] += 1
elif self.rank[x_p] < self.rank[y_p]:
self.parent[x_p] = y_p
else:
self.parent[y_p] = x_p
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
disjoint_set = DisjointSet(len(isConnected))
for i in range(len(isConnected)):
for j in range(i, len(isConnected)):
if isConnected[i][j] == 1:
disjoint_set.union(i, j)
return len(set([disjoint_set.find(i) for i in range(len(isConnected))]))
LC. 128 Longest Consecutive Sequence
class DisjointSet:
def __init__(self, nums):
self.parent = {n:n for n in nums}
self.rank = {n:0 for n in nums}
self.length = {n:1 for n in nums}
self.max_len = 0
def find(self, x):
if x == self.parent[x]:
return x
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
x_p, y_p = self.find(x), self.find(y)
if x_p == y_p:
return
if self.rank[x_p] == self.rank[y_p]:
self.parent[x_p] = y_p
self.length[y_p] += self.length[x_p]
self.rank[y_p] += 1
self.max_len = max(self.max_len, self.length[y_p])
elif self.rank[x_p] < self.rank[y_p]:
self.parent[x_p] = y_p
self.length[y_p] += self.length[x_p]
self.max_len = max(self.max_len, self.length[y_p])
else:
self.parent[y_p] = x_p
self.length[x_p] += self.length[y_p]
self.max_len = max(self.max_len, self.length[x_p])
def max_length(self):
root_counter = {}
for n in self.parent:
root_counter[self.find(n)] = root_counter.get(self.find(n), 0) + 1
return root_counter[max(root_counter, key= lambda x:root_counter[x])]
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
disjoint_set = DisjointSet(nums)
visited = set()
for i, n in enumerate(nums):
if n + 1 in visited:
disjoint_set.union(n, n+1)
if n - 1 in visited:
disjoint_set.union(n, n-1)
visited.add(n)
# return disjoint_set.max_len
return disjoint_set.max_length()